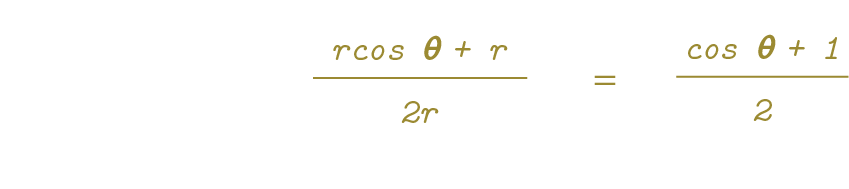How to Calculate
the Phase
of the Moon





How to Calculate
the Phase
of the Moon

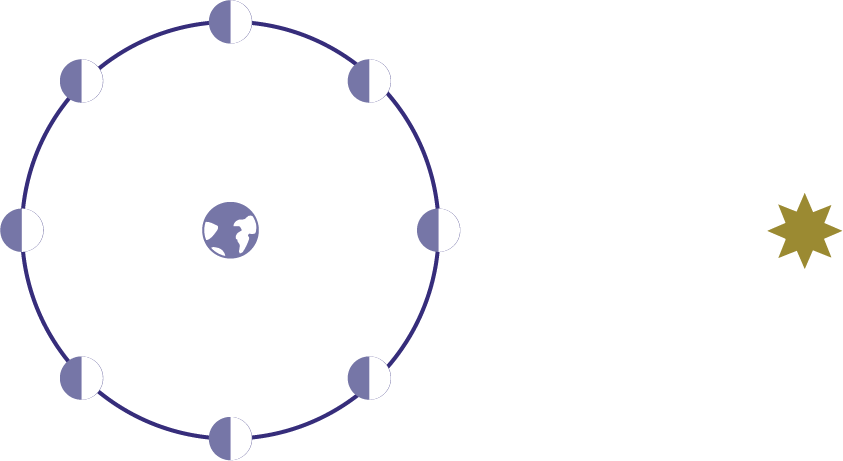

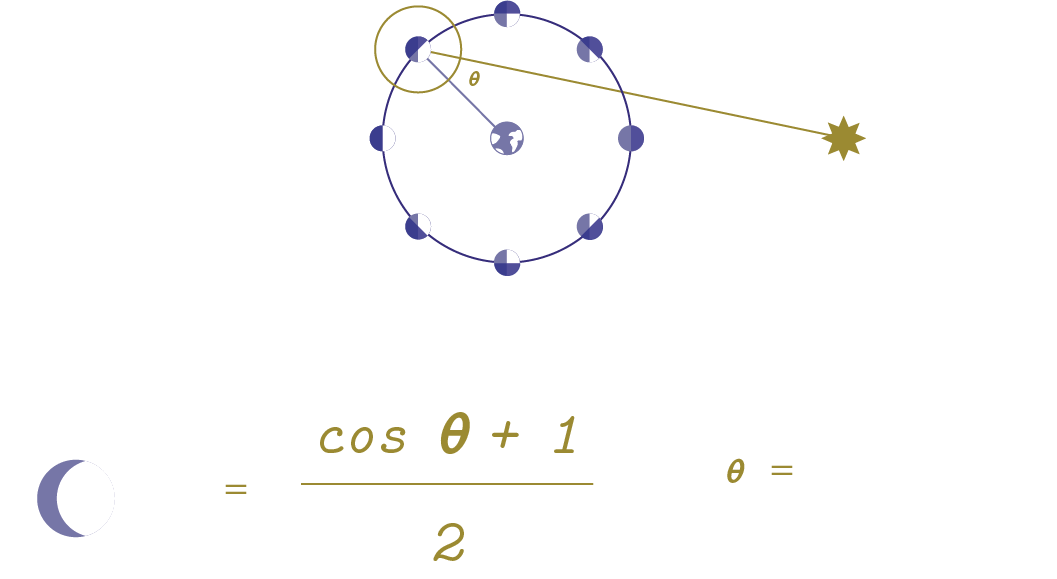
new moon:
side that faces Earth is completely unlit by the Sun

quarter moon:
side that faces Earth is half lit by the Sun

full moon:
side that faces Earth is completely lit by the Sun
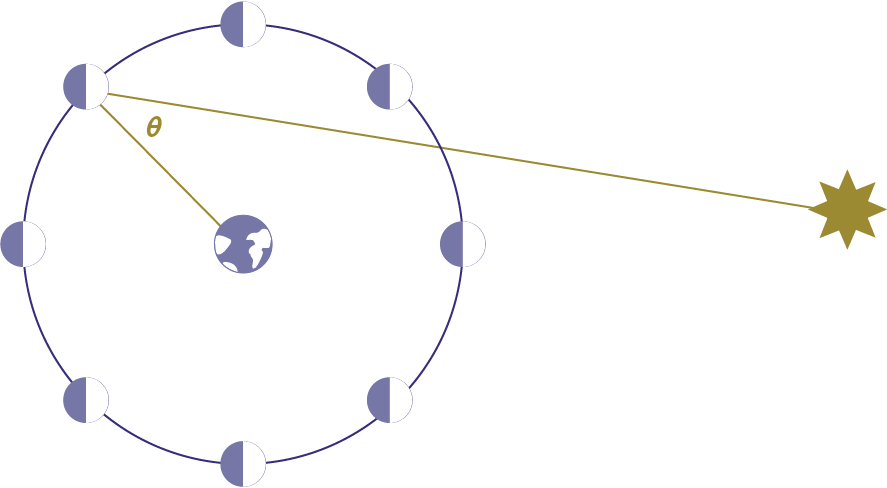
Here we have the Sun, the Earth, and the Moon, which orbits around the Earth.
As the Moon orbits around the Earth, the side facing the Sun is the only side that is illuminated.
The Earth can see vartying amounts of that illumination, depending on where the Moon is in its orbiting cycle.
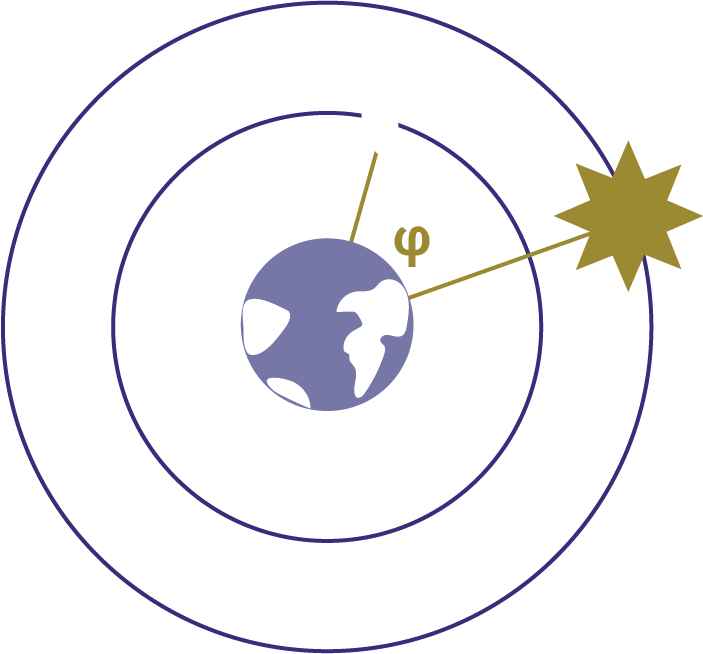
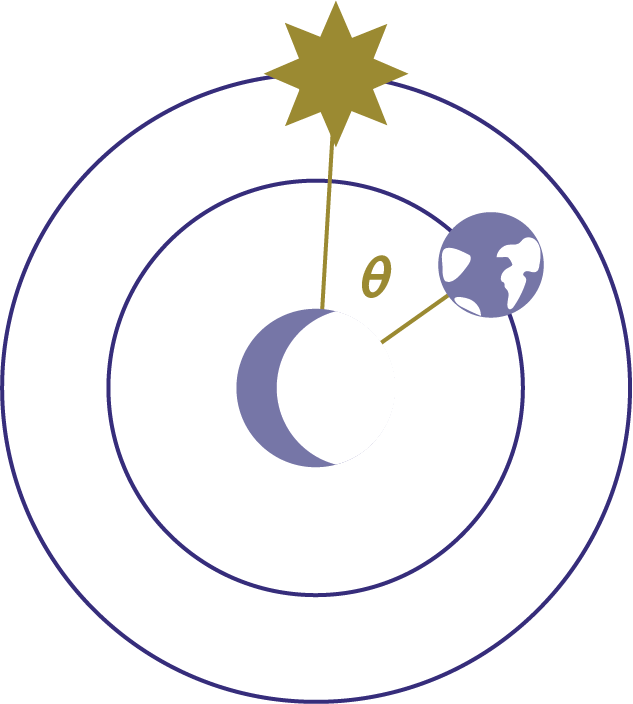
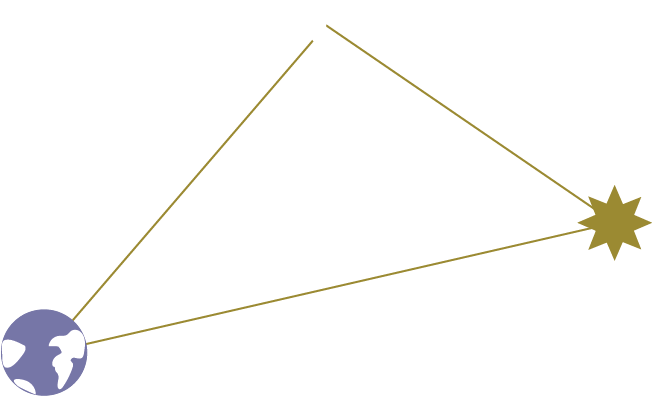
The Moon, Earth, and Sun are 3 points in space, so they form a triangle.
We can fill in the lengths and angles that we know, and use trig to find the rest of the measurements.
a
b
phi
c
c
a One of the sides of the triangle has the length equal to the distance between the Moon and the Earth. This is a known distance, and this distance doesn’t change as the Moon revolves around the Earth and the Earth revolves around the Sun.
b The distance between the Earth and the Sun is also a known fixed distance, so we know the length of that side of the triangle.
The last side of this triangle will change in length depending on the angles between the Earth, Moon, and Sun. Do we know any of those angles?
𝞅 Earlier, we discussed phi or 𝞅, the angle that the Moon and Sun form from the point of view of the Earth. This angle is something that we can observe, given that we are on Earth. Since it's something that we can observe and measure, even though it's not a constant value, let’s count that as a known.
With this known information, we can calculate the last side, c, with the Law of Cosines.
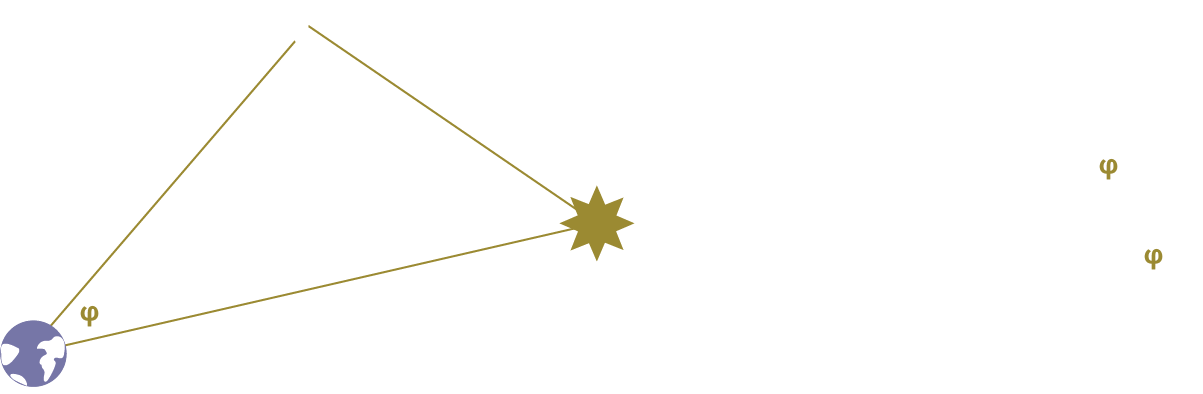
So given that we know the values for 𝞅, a, and b, c, the distance between the Moon and the Sun, is the square root of a squared plus b squared minus 2ab cosine 𝞅.
Now that we know the length of c, we can calculate 𝞱, the angle between the Earth and the Sun from the Moon’s point of view. We can calculate it using the Law of Sines.
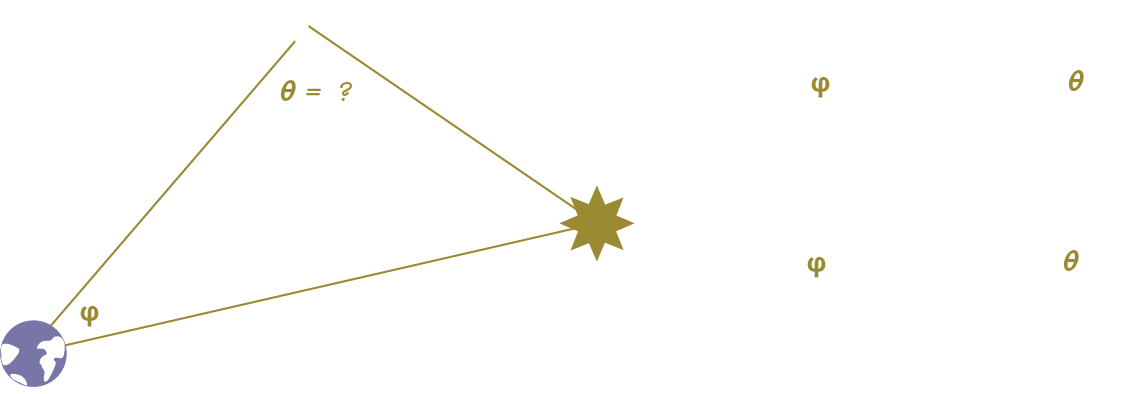
We can substitute the value of c we calculated from the Law of Cosines and then this answer for the sine of 𝞱. Knowing the sine of 𝞱, 𝞱 is then the arcsine of that value.

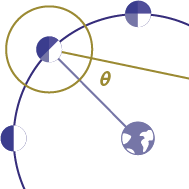
Now we know how to calculate 𝞱, the angle between the Earth and Sun from the point of view of the Moon.
You might notice that as the Moon revolves around the Earth and changes phase, 𝞱 changes too.
Can we find an equation to describe the relationship between 𝞱 and the fraction of the Moon that’s illuminated?
To make it clearer what part of the Moon is illuminated from Earth, we’re adding a color key.
You might notice that as the Moon revolves around the Earth and changes phase, 𝞱 changes too. Can we find the equation that describes the relationship between 𝞱 and the fraction of the Moon that’s illuminated?
To make it clearer what part of the Moon is illuminated from the Earth, we’re adding a color key. The white area is the part illuminated by the Sun, the grey purple area is the area not illuminated by the Sun. Then finally, the dark purple covers the side of the Moon that faces away from the Earth. So the white area that’s left is what we can see of the Moon from the Earth’s point of view.
Let’s zoom in and try to figure out how the angle of the lit area of the Moon is related to 𝞱 for an arbitrary value of 𝞱.
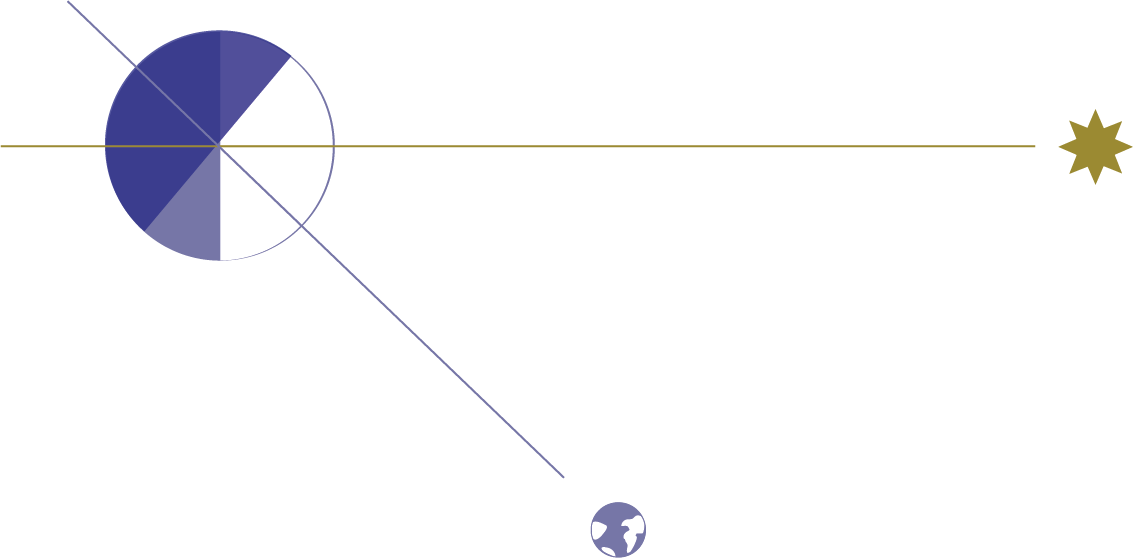
Let's zoom in on the previous illustration, remembering that 𝞱 is the angle between the Sun and Earth from the POV of the Moon.
Let's use this diagram to figure out how the lit area of the Moon is related to 𝞱, for an abitrary value of 𝞱.
We know the Sun lights exactly half of the Moon and forms a perpendicular with the side of the Moon that is lit, so let's mark that.
That perpendicular means that we can mark this lower lit area as having angle 90-𝞱.
The Earth also forms a perpendicular with the side of the Moon that is visible from the Earth, so we can mark that as well.
That means we can mark this upper lit area as having angle 90-𝞱, too.
So, no matter what position the Moon is in its orbit, the lit portion of the Moon has an angle of (90-𝞱) + 90 + (90-𝞱) = 180-𝞱 or 𝝿 - 𝞱 in radians.
The Earth also forms a perpendicular with the side of the Moon that is visible from Earth, so we can mark that as well. That perpendicular means that we can mark this upper lit area as having angle 90-𝞱 as well.
So added up, the lit area of the Moon has the angle 180-𝞱 or in radians, 𝝿 - 𝞱.


From our last step, we now have the angle of the illuminated portion of the Moon, in terms of 𝞱.
So, let's use that to calculate the percentage of illumination of the Moon in terms of 𝞱.
Naively, we can calculate the fraction of the Moon illuminated as the angle illuminated, which is 𝝿 - 𝞱, divided by the total angle of the Moon visible, which is 180 degrees or 𝝿.
But, this doesn’t accurately describe the illuminated percent that we see, because the Moon is a sphere, not a circle.
We need to take into account the Moon’s curvature and how our eyes perceive that curvature.
But, this doesn’t accurately describe the illuminated percent that we see, because the Moon is a sphere, not a circle. And we need to take into account the Moon’s curvature and how our eyes perceive that curvature.




Instead of using the illuminated angle or arc of the Moon, we want to use the length of the projection of the curved surface of the Moon that our eye sees.
How do we calculate the length of this projection?
We know from a previous step that the angle of the projected arc is 𝝿 - 𝞱.
Let’s also assume we know the radius of the Moon, which is a known value.
When we project r down, we see that it's a portion of the distance we care about.
What is the other portion?
The other portion of the distance is the top leg of this right triangle
With hypotenuse equal to r, the radius of the Moon
The triangle's inner angle must be 𝞱, since it forms a straight line with the angle of the lit area of the Moon, 𝝿 - 𝞱
We know from trig that length of the adjacent side to an angle in any right triangle is the hypotenuse times the cosine of that angle.
We can project down to the distance we care about.
Added together, now we know the length of the projection of the illuminated portion of the Moon.
Let’s assume we know the radius of the Moon, which we do. The radius, r is going to be a portion of the distance we care about. What is the other portion? The other portion of the distance is a leg of this right triangle with hypotenuse r and inner angle 𝞱.
We know from the definition of the cosine that length of the adjacent side to an angle in any right triangle is the hypotenuse times the cosine of that angle. So now we know the length of that side of the right triangle, which we can project down to the distance we care about. Now we know the length of the projection of the illuminated area of the Moon as seen on Earth.